collapse is a C/C++ based package for data transformation and statistical computing in R. Among other features it introduces an excellent and highly efficient architecture for grouped (and weighted) statistical programming in R. This post briefly explains this architecture and demonstrates:
How to program highly efficient grouped statistical computations and data manipulations in R using the grouped functions supplied by collapse.
How to use the grouping mechanism of collapse with custom C/C++ code to create further efficient grouped functions/operations in R.
Essentials: collapse Grouping Objects
collapse uses grouping objects as essential inputs for grouped computations. These objects are created from vectors or lists of vectors (i.e. data frames) using the function GRP():
library(collapse)
# A dataset supplied with collapse providing sectoral value added (VA) and employment (EMP)
head(GGDC10S, 3)
## Country Regioncode Region Variable Year AGR MIN MAN PU CON WRT TRA FIRE GOV OTH SUM
## 1 BWA SSA Sub-saharan Africa VA 1960 NA NA NA NA NA NA NA NA NA NA NA
## 2 BWA SSA Sub-saharan Africa VA 1961 NA NA NA NA NA NA NA NA NA NA NA
## 3 BWA SSA Sub-saharan Africa VA 1962 NA NA NA NA NA NA NA NA NA NA NA
fdim(GGDC10S)
## [1] 5027 16
# Creating a grouping object (by default return.order = FALSE as the ordering is typically not needed)
g <- GRP(GGDC10S, c("Country", "Variable"), return.order = TRUE)
# Printing it
print(g)
## collapse grouping object of length 5027 with 85 ordered groups
##
## Call: GRP.default(X = GGDC10S, by = c("Country", "Variable"), return.order = TRUE), X is unordered
##
## Distribution of group sizes:
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4.00 53.00 62.00 59.14 63.00 65.00
##
## Groups with sizes:
## ARG.EMP ARG.VA BOL.EMP BOL.VA BRA.EMP BRA.VA
## 62 62 61 62 62 62
## ---
## VEN.EMP VEN.VA ZAF.EMP ZAF.VA ZMB.EMP ZMB.VA
## 62 63 52 52 52 52
# Plotting it
plot(g)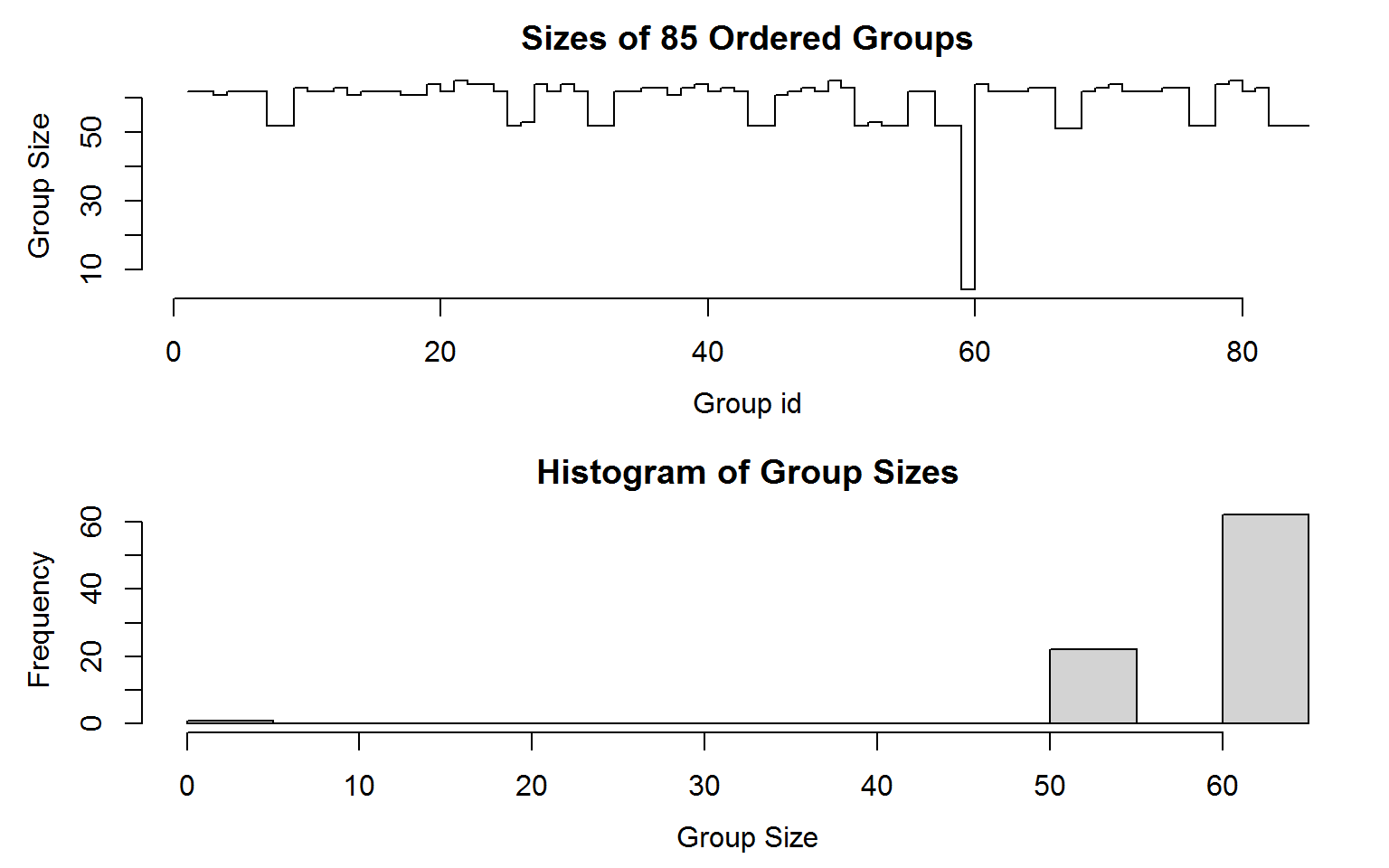
Grouping is done very efficiently using radix-based ordering in C (thanks to data.table source code). The structure of this object is shown below:
str(g)
## List of 8
## $ N.groups : int 85
## $ group.id : int [1:5027] 8 8 8 8 8 8 8 8 8 8 ...
## $ group.sizes: int [1:85] 62 62 61 62 62 62 52 52 63 62 ...
## $ groups :'data.frame': 85 obs. of 2 variables:
## ..$ Country : chr [1:85] "ARG" "ARG" "BOL" "BOL" ...
## .. ..- attr(*, "label")= chr "Country"
## .. ..- attr(*, "format.stata")= chr "%9s"
## ..$ Variable: chr [1:85] "EMP" "VA" "EMP" "VA" ...
## .. ..- attr(*, "label")= chr "Variable"
## .. ..- attr(*, "format.stata")= chr "%9s"
## $ group.vars : chr [1:2] "Country" "Variable"
## $ ordered : Named logi [1:2] TRUE FALSE
## ..- attr(*, "names")= chr [1:2] "GRP.sort" "initially.ordered"
## $ order : int [1:5027] 2583 2584 2585 2586 2587 2588 2589 2590 2591 2592 ...
## ..- attr(*, "starts")= int [1:85] 1 63 125 186 248 310 372 424 476 539 ...
## ..- attr(*, "maxgrpn")= int 65
## ..- attr(*, "sorted")= logi FALSE
## $ call : language GRP.default(X = GGDC10S, by = c("Country", "Variable"), return.order = TRUE)
## - attr(*, "class")= chr "GRP"The first three slots of this object provide the number of unique groups, a group-id matching each value/row to a group1, and a vector of group-sizes. The fourth slot provides the unique groups (default return.groups = TRUE), followed by the names of the grouping variables, a logical vector showing whether the grouping is ordered (default sort = TRUE), and the ordering vector which can be used to sort the data alphabetically according to the grouping variables (default return.order = FALSE).
Grouped Programming in R
collapse provides a whole ensemble of C++ based generic statistical functions that can use these ‘GRP’ objects to internally perform (column-wise) grouped (and weighted) computations on vectors, matrices and data frames in R. Their names are contained in the global macro .FAST_FUN:
.FAST_FUN
## [1] "fmean" "fmedian" "fmode" "fsum" "fprod" "fsd" "fvar"
## [8] "fmin" "fmax" "fnth" "ffirst" "flast" "fNobs" "fNdistinct"
## [15] "fscale" "fbetween" "fwithin" "fHDbetween" "fHDwithin" "flag" "fdiff"
## [22] "fgrowth"Additional functions supporting grouping objects are TRA (grouped replacing and sweeping out statistics), BY (split-apply-combine computing) and collap (advanced data aggregation with multiple functions).
To provide a brief example, we can compute a grouped mean of the above data using:
head(fmean(GGDC10S[6:16], g))
## AGR MIN MAN PU CON WRT TRA
## ARG.EMP 1419.8013 52.08903 1931.7602 101.720936 742.4044 1982.1775 648.5119
## ARG.VA 14951.2918 6454.94152 36346.5456 2722.762554 9426.0033 26633.1292 14404.6626
## BOL.EMP 964.2103 56.03295 235.0332 5.346433 122.7827 281.5164 115.4728
## BOL.VA 3299.7182 2846.83763 3458.2904 664.289574 729.0152 2757.9795 2727.4414
## BRA.EMP 17191.3529 206.02389 6991.3710 364.573404 3524.7384 8509.4612 2054.3731
## BRA.VA 76870.1456 30916.64606 223330.4487 43549.277879 70211.4219 178357.8685 89880.9743
## FIRE GOV OTH SUM
## ARG.EMP 627.79291 2043.471 992.4475 10542.177
## ARG.VA 8547.37278 25390.774 7656.3565 152533.839
## BOL.EMP 44.56442 NA 395.5650 2220.524
## BOL.VA 1752.06208 NA 4383.5425 22619.177
## BRA.EMP 4413.54448 5307.280 5710.2665 54272.985
## BRA.VA 183027.46189 249135.452 55282.9748 1200562.671By default (use.g.names = TRUE), group names are added as names (vectors) or row-names (matrices and data frames) to the result. For data frames we can also add the grouping columns again using2:
head(add_vars(g[["groups"]], fmean(get_vars(GGDC10S, 6:16), g, use.g.names = FALSE)))
## Country Variable AGR MIN MAN PU CON WRT TRA
## 1 ARG EMP 1419.8013 52.08903 1931.7602 101.720936 742.4044 1982.1775 648.5119
## 2 ARG VA 14951.2918 6454.94152 36346.5456 2722.762554 9426.0033 26633.1292 14404.6626
## 3 BOL EMP 964.2103 56.03295 235.0332 5.346433 122.7827 281.5164 115.4728
## 4 BOL VA 3299.7182 2846.83763 3458.2904 664.289574 729.0152 2757.9795 2727.4414
## 5 BRA EMP 17191.3529 206.02389 6991.3710 364.573404 3524.7384 8509.4612 2054.3731
## 6 BRA VA 76870.1456 30916.64606 223330.4487 43549.277879 70211.4219 178357.8685 89880.9743
## FIRE GOV OTH SUM
## 1 627.79291 2043.471 992.4475 10542.177
## 2 8547.37278 25390.774 7656.3565 152533.839
## 3 44.56442 NA 395.5650 2220.524
## 4 1752.06208 NA 4383.5425 22619.177
## 5 4413.54448 5307.280 5710.2665 54272.985
## 6 183027.46189 249135.452 55282.9748 1200562.671The execution cost of all of these functions is extremely small, so the performance is essentially limited by C++, not by R.
library(microbenchmark)
microbenchmark(call = add_vars(g[["groups"]], fmean(get_vars(GGDC10S, 6:16), g, use.g.names = FALSE)))
## Unit: microseconds
## expr min lq mean median uq max neval
## call 394.038 434.6465 582.3857 471.685 566.959 2403.495 100We can use these functions to write very efficient grouped code in R. This shows a simple application in panel data econometrics comparing a pooled OLS to a group means, a between and a within estimator computed on the demeaned data3:
Panel_Ests <- function(formula, data, pids, weights = NULL, ...) {
# Get variables as character string, first variable is dependent variable
vars <- all.vars(formula)
# na_omit is a fast replacement for na.omit
data_cc <- na_omit(get_vars(data, c(vars, pids, weights)))
# Create grouped object (pids should be a character vector)
g <- GRP(data_cc, pids, return.groups = FALSE, call = FALSE)
# Getting weights from data (weights should be character string)
if(length(weights)) weights <- .subset2(data_cc, weights)
# qM is a faster as.matrix
data_cc <- qM(get_vars(data_cc, vars))
# Computing group means
mean_data_cc <- fmean(data_cc, g, weights, use.g.names = FALSE)
# This computes regression coefficients, dots options regard different fitting methods
reg <- function(x, w = weights, ...)
drop(flm(x[, 1L], x[, -1L, drop = FALSE], w, add.icpt = TRUE, ...))
qM(list(Pooled = reg(data_cc),
Means = reg(mean_data_cc, w = if(length(weights)) fsum(weights, g) else NULL),
# This replaces data values with the group-mean -> between-group estimator
Between = reg(TRA(data_cc, mean_data_cc, "replace_fill", g)),
# This subtracts the group-means -> within-group estimator
Within = reg(TRA(data_cc, mean_data_cc, "-", g))))
}
library(magrittr) # Pipe operators
# Calculating Value Added Percentage Shares (data is in local currency)
VA_shares <- fsubset(GGDC10S, Variable == "VA") %>% ftransformv(6:16, `*`, 100/SUM)
# Value Added data (regressing Government on Agriculture, Manufactoring and Finance & Real Estate)
Panel_Ests(GOV ~ AGR + MAN + FIRE, VA_shares, "Country") %>% round(4)
## Pooled Means Between Within
## (Intercept) 25.8818 26.6702 26.5828 0.0000
## AGR -0.3425 -0.3962 -0.3749 -0.2124
## MAN -0.2339 -0.1744 -0.2215 -0.2680
## FIRE -0.2083 -0.3337 -0.2572 -0.0742
# Employment data
fsubset(GGDC10S, Variable == "EMP") %>% ftransformv(6:16, `*`, 100/SUM) %>%
Panel_Ests(formula = GOV ~ AGR + MAN + FIRE, "Country") %>% round(4)
## Pooled Means Between Within
## (Intercept) 33.2047 34.6626 35.4332 0.0000
## AGR -0.3543 -0.3767 -0.3873 -0.2762
## MAN -0.4444 -0.4595 -0.4790 -0.4912
## FIRE -0.1721 -0.3097 -0.2892 -0.1087A benchmark below shows that this series of estimators is executed very efficiently and scales nicely to large data (quite a bit faster than using plm to do it).
VA_shares$weights <- abs(rnorm(fnrow(VA_shares))) # Random weights
# Benchmark on VA data
microbenchmark(lm.fit = Panel_Ests(SUM ~ AGR + MIN + MAN, VA_shares, "Country"),
chol = Panel_Ests(SUM ~ AGR + MIN + MAN, VA_shares, "Country", method = "chol"),
lm.fit.w = Panel_Ests(SUM ~ AGR + MIN + MAN, VA_shares, "Country", "weights"),
chol.w = Panel_Ests(SUM ~ AGR + MIN + MAN, VA_shares, "Country", "weights", method = "chol"))
## Unit: milliseconds
## expr min lq mean median uq max neval cld
## lm.fit 1.490470 1.663838 2.185618 1.942743 2.187956 9.982579 100 a
## chol 1.469943 1.668300 2.161204 1.903919 2.140430 8.107889 100 a
## lm.fit.w 1.686819 1.926232 2.469664 2.243068 2.611892 10.030328 100 a
## chol.w 1.719842 1.935603 2.500210 2.326963 2.647592 7.600058 100 aThere are lots and lots of other applications that can be devised in R using the .FAST_FUN and efficient programming with grouping objects.
Creating Grouped Functions in C/C++
It is also possible to just use ‘GRP’ objects as input to new grouped functions written in C or C++. Below I use Rcpp to create a generic grouped anyNA function for vectors:
// [[Rcpp::plugins(cpp11)]]
#include <Rcpp.h>
using namespace Rcpp;
// Inputs:
// x - A vector of any type
// ng - The number of groups - supplied by GRP() in R
// g - An integer grouping vector - supplied by GRP() in R
// Output: A plain logical vector of size ng
template <int RTYPE>
LogicalVector ganyNACppImpl(Vector<RTYPE> x, int ng, IntegerVector g) {
int l = x.size();
if(l != g.size()) stop("length(x) must match length(g)");
LogicalVector out(ng); // Initializes as false
if(RTYPE == REALSXP) { // Numeric vector: all logical operations on NA/NaN evaluate to false, except != which is true.
for(int i = 0; i < l; ++i) {
if(x[i] != x[i] && !out[g[i]-1]) out[g[i]-1] = true;
}
} else { // other vectors
for(int i = 0; i < l; ++i) {
if(x[i] == Vector<RTYPE>::get_na() && !out[g[i]-1]) out[g[i]-1] = true;
}
}
return out;
}
// Disabling complex and non-atomic vector types
template <>
LogicalVector ganyNACppImpl(Vector<CPLXSXP> x, int ng, IntegerVector) {
stop("Not supported SEXP type!");
}
template <>
LogicalVector ganyNACppImpl(Vector<VECSXP> x, int ng, IntegerVector) {
stop("Not supported SEXP type!");
}
template <>
LogicalVector ganyNACppImpl(Vector<RAWSXP> x, int ng, IntegerVector) {
stop("Not supported SEXP type!");
}
template <>
LogicalVector ganyNACppImpl(Vector<EXPRSXP> x, int ng, IntegerVector) {
stop("Not supported SEXP type!");
}
// [[Rcpp::export]]
LogicalVector ganyNACpp(const SEXP& x, int ng = 0, const IntegerVector& g = 0){
RCPP_RETURN_VECTOR(ganyNACppImpl, x, ng, g);
}
On the R side things are then pretty simple:
library(Rcpp)
sourceCpp("ganyNA.cpp")
ganyNA <- function(x, g, use.g.names = TRUE, ...) {
# Option group.sizes = FALSE prevents tabulation of levels if a factor is passed
g <- GRP(g, return.groups = use.g.names, group.sizes = FALSE, call = FALSE, ...)
res <- ganyNACpp(x, g[[1L]], g[[2L]])
# GRPnames creates unique group names. For vectors they need not be character typed.
if(use.g.names) names(res) <- GRPnames(g, force.char = FALSE)
res
}Regarding the grouping step, there are actually different options to set this up: GRP() is a S3 generic function with a default method applying to atomic vectors and lists / data frames, but also a ‘factor’ method converting factors to ‘GRP’ objects. Above I have used the generic GRP function with the option group.sizes = FALSE, so factors are efficiently converted without tabulating the levels. This provides more efficiency if a factor is passed to g. Since collapse 1.4.0, the factor method additionally supports efficient dropping of unused factor levels through setting an argument drop = TRUE, which internally calls a C++ function function fdroplevels on the factor. By default drop = FALSE and this default is kept here. The cost of dropping levels on a large factor can be seen in the benchmark below.
While the generic version of GRP() offers a lot of flexibility and faster methods for grouping different objects (for example you can also apply GRP() on a grouped tibble to get at ‘GRP’ object from the attached ‘groups’ attribute), a viable alternative is to just use the default method g <- GRP.default(g, return.groups = use.g.names, call = FALSE). This will get rid of unused factor levels, but using factors for grouping is just as efficient as any other vector.
GGDC10S %$% ganyNA(SUM, list(Country, Variable)) %>% head
## ARG.EMP ARG.VA BOL.EMP BOL.VA BRA.EMP BRA.VA
## FALSE FALSE FALSE TRUE FALSE TRUE
# 10 million obs and 1 million groups, 1% of data missing
x <- na_insert(rnorm(1e7), prop = 0.01)
g <- sample.int(1e6, 1e7, TRUE)
system.time(ganyNA(x, g))
## user system elapsed
## 0.82 0.04 0.84
system.time(ganyNA(x, g, use.g.names = FALSE))
## user system elapsed
## 0.57 0.06 0.64
# Using a factor grouping variable: more efficient
f <- qF(g, na.exclude = FALSE) # Efficiently creating a factor (qF is faster as.factor)
system.time(ganyNA(x, f))
## user system elapsed
## 0.03 0.01 0.04
system.time(ganyNA(x, f, drop = TRUE)) # This also checks for unused levels and drops them (if found)
## user system elapsed
## 0.13 0.03 0.15
# Note: use.g.names = FALSE does not give a performance improvement with factors because unique factor levels are already computed
# We can also efficiently pass a 'GRP' object: both GRP.GRP and GRP.default simply return it.
g <- GRP(g)
system.time(ganyNA(x, g))
## user system elapsed
## 0.03 0.00 0.03
system.time(ganyNA(x, g, use.g.names = FALSE))
## user system elapsed
## 0.04 0.00 0.05We could additionally add a TRA argument and then internally call the TRA() function to allow for replacing and sweeping out statistics, but this does not make much sense here.
By default (
sort = TRUE) the grouping is ordered, which is equivalent to data.table grouping withkeyby.↩︎add_varsis a faster alternative tocbindandget_varsis a faster alternative to[.data.framefor subsetting columns.↩︎A random effects estimator could easily be added, see the example here.↩︎